Условие:
Заданы параметры сопла Лаваля (Таблица 1):
1) начальное давление рабочего тела р1=14 am;
2) начальная температура Т1=630 °К;
3) начальная скорость с1=150 м/сек;
4) массовый расход рабочего тела 𝑚̇=25 кг/сек;
5) давление в выходном сечении сопла р2=2,0 ат;
6) угол между образующими конуса в расширяющейся части сопла 𝜑=9°;
7) рабочее тело − двухатомный газ с 𝓀 =1,4. (воздух, R=287 Дж/кг·К)
Таблица 1. Исходные данные расчета сопла Лаваля.

Требуется:
1. Рассчитать параметры торможения.
2. Определить основные параметры в характерных сечениях сопла (входное‚ критическое и выходное).
3. Рассчитать общую длину сопла.
4. В сужающейся части сопла разбить его длину на пять интервалов, примерно равных. Два последних интервала (ближних к минимальному сечению) разбить пополам. Во всех этих точках по формуле (18) определить профиль сопла, из табл. 2.1 − газодинамические функции и изменение основных параметров по длине. Результаты расчетов свести в табл. 2.2.
5. B сверхзвуковой части сопла разбить перепад по давлению между ркр, и p2 так, чтобы получить не менее пяти промежуточных точек. По табл. 2.1 в промежуточных точках найти газодинамические функции, рассчитать изменение основных параметров по длине. Все данные расположить в табл. 2.3.
6. Предположим, что в минимальном (критическом) сечении сопла имеет место скачок уплотнения. При этом в расширяющейся части сопла будет дозвуковое течение, хотя скорость звука достигается в критическом сечении. Профиль сопла оставим неизменным. Можно рассчитать q(𝜆), a по ней все газодинамические функции. Так как при слабом скачке параметры торможения постоянны, нетрудно рассчитать основные параметры и их изменение по длине сопла. Результаты расчетов занести в табл. 2.4.
7. Предположим, что скачок имеет место в одном из сечений внутри сопла. Тогда по формуле (21) определяем коэффициент скорости 𝜆𝑐′ за скачком. По формуле (22) вычисляем параметры торможения до скачка и газодинамические функции. Удобнее располагать скачок в одном из сечений,
которые имели место при расчете режима истечения газа из сопла. Скачки необходимо рассчитывать не менее чем в трех сечения внутри сопла. Эффективные результаты дают расчеты примерно с третьего сечения (считая от критического). Результаты вычислений можно свести в табл. 2.4. Очевидно, что данная методика обратима и по ней нетрудно рассчитать сопло со скачком при заданном противодавлении на выходе из сопла.
8. По рассчитанным значениям в масштабе построить графики изменения d, F, p, ⍴, T, с, М по длине сопла с расчетными и нерасчетными режимами истечения из сопла.
Решение:
Допущения:
Теплофизические свойства рабочего тела неизменны:
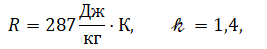
Удельная изобарная теплоёмкость воздуха
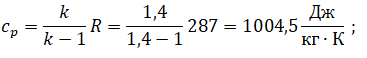
Рабочее тело идеальный газ;
Течение энергоизолированно во всей области течения;
Течение обратимо, и...
