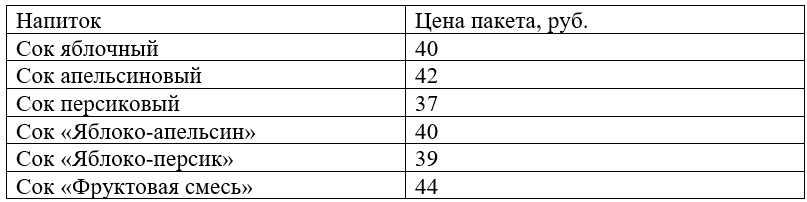
Предприятие производит фруктовые соки и продает их упакованными в пакеты емкостью 1 л. Список продукции и цена реализации за один пакет приведены в табл. Сок «Яблоко-апельсин» содержит 70% яблочного и 30% апельсинового сока, «Яблоко-персик» - 60%

Предприятие производит фруктовые соки и продает их упакованными в пакеты емкостью 1 л. Список продукции и цена реализации за один пакет приведены в табл.

Сок «Яблоко-апельсин» содержит 70% яблочного и 30% апельсинового сока, «Яблоко-персик» - 60% яблочного и 40% персикового сока, «Фруктовая смесь» – 50% яблочного, 20% апельсинового и 30% персикового сока.

В настоящий момент на складе предприятия имеются концентраты для приготовления 2800 л яблочного сока, 1900 л апельсинового сока и 2500 л персикового сока.

Себестоимость приготовления 1 л яблочного сока составляет 20 руб., апельсинового – 23 руб., персикового – 18 руб.

Предприятие имеет заказ на 600 пакетов яблочного сока, 300 пакетов сока «Яблоко-апельсин» и 1000 пакетов сока «Фруктовая смесь». Заказ должен быть выполнен в текущую поставку. Кроме того, из опыта известно, что ни один из видов продукции не следует производить в количестве более чем 2 тыс. пакетов.

Задания

1) Найти план производства, обеспечивающий наибольшую прибыль.

2) Для найденного оптимального плана получить отчет об устойчивости. Объяснить, что означают нормированные стоимости соков яблочного, «Яблоко-апельсин» и «Фруктовая смесь». Сколько пакетов яблочного сока и сока «Яблоко-апельсин» следовало бы произвести, если бы заказ на эти две позиции отсутствовал?

3) Пусть имеется возможность закупить концентрат для получения дополнительных 200 литров одного из соков. Концентрат какого сока (яблочного, апельсинового или персикового) следует предпочесть? Какую величину дополнительной прибыли можно будет получить по сравнению с первоначальным планом? Для ответа на данные вопросы использовать отчет об устойчивости.