Условие:
1. Доказать, что если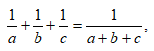 
то для любого нечетного n справедливо тождество
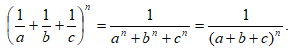
2. Доказать, что если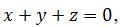
то
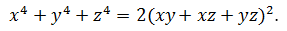
3. Доказать, что если
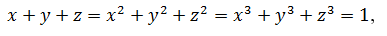
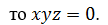
Решение:
1. Равенство
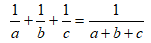
Можно записать в виде
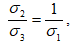
т.е , или Таким образом хотя бы одно из выражений равно нулю, т.е. имеет место хотя бы одно из равенств Но в таком случае равенства