Условие:
1. Упростить платежную матрицу 1, используя принцип доминирования и дублирования стратегий. Графическим методом найти решение игры.
2. Найти решение игры с заданными платежными матрицами 2 и 3, сведя ее к задаче линейного программирования
3. Найти решение игры, заданной матрицей в задании 1, методом Брауна-Робинсона. Число итерация равно 10.
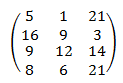
Решение:
1)
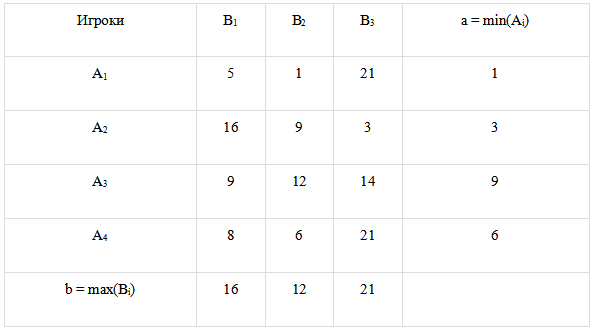
a = max(ai) = 9, b = min(bj) = 12.
a b, тогда цена игры находится в пределах 9 y 12. Находим решение игры в смешанных стратегиях.
Проверяем платежную матрицу на доминирующие строки и доминирующие столбцы.
