1. Главная
  2. Библиотека
  3. Высшая математика
  4. 1. В классе 23 учащихся, из которых 14 девушек. Выбираются делегаты на общешкольное собрание. Среди делегатов должно быть...

1. В классе 23 учащихся, из которых 14 девушек. Выбираются делегаты на общешкольное собрание. Среди делегатов должно быть 4 девушки и 4 юноши. Сколько списков делегатов может быть представлено?

«1. В классе 23 учащихся, из которых 14 девушек. Выбираются делегаты на общешкольное собрание. Среди делегатов должно быть 4 девушки и 4 юноши. Сколько списков делегатов может быть представлено?»
  • Высшая математика

Условие:

1. В классе 23 учащихся, из которых 14 девушек. Выбираются делегаты на общешкольное собрание. Среди делегатов должно быть 4 девушки и 4 юноши. Сколько списков делегатов может быть представлено?

2. Из колоды, содержащей 52 карты, выбирается 8 карт. Найти количество выборок, в которых будет присутствовать один король и ровно две карты треф.

3. На почте есть в продаже открытки «С праздником 8 марта» пяти видов. Требуется купить для поздравления 7 открыток. Сколькими способами это можно сделать?

Решение:

Для двух первых задач число всевозможных случаев будет определяться числом сочетаний из n по k:

.

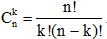Если объекты разделены на k групп, содержащих n1, n2, ..., nk объектов (n1+n2+...nk = n) число способов выбрать из них соответственно m1, m2, ..., mk объектов (m1+m2+... + mk) равно:

.

Похожие задачи

Не нашел нужную задачу?

Воспользуйся поиском

AI помощники

Выбери предмет

E
S
А
Б
В
Г
Д
Е
Ж
З
И
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Э
Я