Условие задачи
1. Получить 100 случайных значений случайной величины, распределенной по заданному закону:
Показательный закон с параметром L = 1
2. Обработать выборку методом «сгруппированных данных" и построить таблицу соответствующего статистического ряда.
3. Вычислить выборочные среднее, дисперсию, асимметрию и эксцесс. Построить гистограмму и график эмпирической функции распределения.
4. Построить доверительные интервалы для выборочного среднего и дисперсии с надежностью 0,95.
5. Проверить статистическую гипотезу о соответствии выборочного закона распределения заданному в п.1 при помощи критериев Пирсона и Колмогорова (уровень значимости 0,05).
6. Даны значения трёх факторов X, Y, Z каждый на двух уровнях (всего 8 наборов значений), для каждого из них известно экспериментальное значение (в задании – случайное). Найти методом полного факторного эксперимента линейное уравнение регрессии.
Ответ
1. Получим 100 случайных чисел, распределенных по показательному закону, с помощью функции СЛЧИС() в Excel и преобразования:
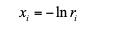
2. Составим вариационный интервальный ряд.
Крайние элементы:
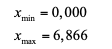
Размах выборки:
