а) Представить данные в виде интервального статистического ряда, проиллюстрировать его гистограммой ni(x). б) Найти эмпирические значения выборочного среднего и дисперсии с точностью 10–2;
- Высшая математика
Условие:
а) Представить данные в виде интервального статистического ряда, проиллюстрировать его гистограммой ni(x).
б) Найти эмпирические значения выборочного среднего и дисперсии с точностью 10–2;
в) Сделать оценки математического ожидания и дисперсии измеренной случайной величины с точностью до единиц.
г) Выдвинуть гипотезу о функциональном виде распределения и значениях его параметров, построить математическую модель в виде предполагаемой функции плотности распределения и интегральной функции распределения.
д) При необходимости, изменить статистический ряд, добиваясь наполненности интервалов ni ≥ 5 и покрытия всей области возможных значений выдвинутой гипотезы.
е) Исходя из выдвинутой гипотезы, получить теоретические предсказания количества измерений ![]() для каждого интервала статистического ряда.
для каждого интервала статистического ряда.
ж) Проиллюстрировать гипотезу графически, построив сравнительную гистограмму распределений эмпирического (ni(x)) и теоретического ![]() количества измерений по интервалам статистического ряда на одном поле.
количества измерений по интервалам статистического ряда на одном поле.
з) Проверить выдвинутую гипотезу с помощью метода χ2 Пирсона, сделать вывод о необходимости отвергнуть гипотезу (на уровне значимости α = 0,05)
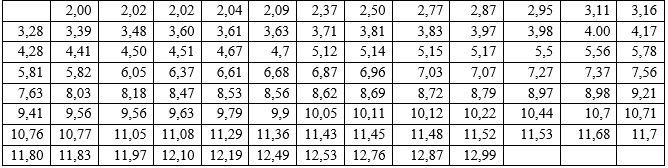
Решение:
а) Представить данные в виде интервального статистического ряда, проиллюстрировать его гистограммой ni(x).
Приемлимое количество интервалов от 6 до 10, желательно выбирать ширину интервалов и границы между ними целыми. У нас минимальное значение в выборке 2, а максимальное не достигает 13. Ширина этого диапазона 13-2=11 единицы, она неудобна для разделения на одинаковые интервалы целой ширины. Однако, немного увеличивая диапазон до 12 (2 14), мы имеем возможности взять 12 интервалов по 1...
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
Выбери предмет
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Текстильная промышленность
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства