Анализируется выборка из 100 малых предприятий региона. Цель обследования – измерение коэффициента соотношения заёмных и собственных средств на каждом предприятии. Результаты представлены в виде таблицы. Таблица - Коэффициенты соотношений заёмных и

Анализируется выборка из 100 малых предприятий региона. Цель обследования – измерение коэффициента соотношения заёмных и собственных средств на каждом предприятии. Результаты представлены в виде таблицы.

Таблица - Коэффициенты соотношений заёмных и собственных средств на предприятиях

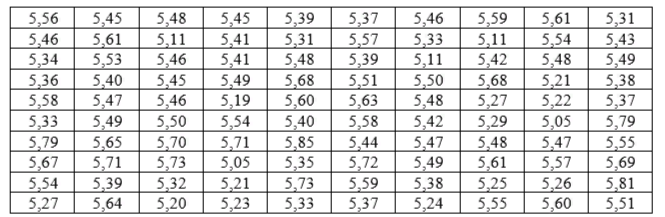
Используя полученные данные, выполните следующие задания.

Задание 1. Постройте статистический ряд.

Задание 2. Вычислите относительные частоты, накопленные относительные частоты, плотности относительных частот.

Задание 3. Представьте графически статистический ряд в виде полигона или гистограммы.

Задание 4. Постройте график накопленных относительных частот.

Задание 5. Запишите эмпирическую функцию распределения.

Задание 6. Вычислите точечные оценки параметров закона распределения: 

1)  выборочное среднее;

2)  выборочную дисперсию (смещённую, т. е. неисправленную, и несмещённую, т. е. исправленную);

3)  выборочное среднее квадратическое отклонение (смещённое и несмещённое);

4)  выборочную моду;

5)  выборочную медиану.

Задание 7. Полагая, что данная генеральная совокупность подчиняется нормальному закону, найдите доверительный интервал для неизвестного математического ожидания при условии, что дисперсия неизвестна, если доверительная вероятность задаётся формулой

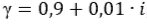
где i = 5.