Условие задачи
Аппроксимировать функцию x = x(t) в пространстве L2(-1;1) двумя способами:
A. При помощи ортогональной тригонометрической системы;
B. При помощи ортогональных многочленов Лежандра.
Число n - заданный порядок аппроксимации. Построить графики функции x и полученных аппроксимаций. Сравнить точность аппроксимаций в метрике пространства L2(-1;1) .
Для вычисления и построения графиков использовать математические пакеты – MATLAB.
1. Построить несколько аппроксимаций при постепенно возрастающем значении n ;
2. Указать особенности функции x(t) , плохо влияющие на качество аппроксимации каждого типа (тригонометрического, полиномиального);
3. Выявить эффект Гиббса, где он есть, указать причину его появления;
4. Установить тип сходимости ряда Фурье к x(t) на промежутке [-1;1] (поточечная, равномерная, среднеквадратичная).
Ответ
Решение этой задачи опирается на теоретические сведения: понятие тригонометрической системы и многочленов Лежандра, определение ряда Фурье и его связь с задачей аппроксимации. Для аппроксимации функции можно использовать частичную сумму ряда Фурье.
А. Тригонометрическая аппроксимация.
Рассмотрим в пространстве L2(-1;1) ортонормированный тригонометрический базис:
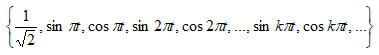
Обозначим символом Trig15(t) частич...
