Условие задачи
Дана функция двух переменных.
а) Для функции из пункта а: найти область определения функции двух переменных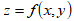 
. Изобразить ее на координатной плоскости XOY и заштриховать.
б) Для функции из пункта б:
1. вычислить частные производные первого порядка и проверить, удовлетворяет ли функция двух переменных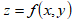 
указанному дифференциальному уравнению первого порядка в частных производных;
2. найти градиент функции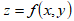 
в точке.
в) найти 
Ответ
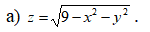
Область определения:
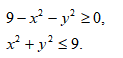
Полученное неравенство определяет множество точек, лежащих внутри и на окружность с центром в начале координат О(0,0) и радиусом r=3.
Потяни
