Дана кривая икс в квадрате минус семь игрек в квадрате минус шесть икс игрек плюс два икс плюс двадцать шесть игрек плюс пятьдесят семь равно ноль
«Дана кривая икс в квадрате минус семь игрек в квадрате минус шесть икс игрек плюс два икс плюс двадцать шесть игрек плюс пятьдесят семь равно ноль»
- Высшая математика
Условие:
Дана кривая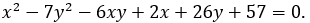 
1. Докажите, что эта кривая – гипербола.
2. Найдите координаты ее центра симметрии.
3. Найдите квадраты ее действительной и мнимой полуосей.
4. Запишите общее уравнение фокальной оси.
5. Постройте данную гиперболу.
Решение:
1. Докажем, что эта кривая гипербола.
Квадратичную форму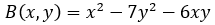
приводим к главным осям. Определяем коэффициенты Записываем матрицу квадратичной формы и находим ее собственные числа. Записываем и решаем характеристическое уравнение матрицы
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
AI помощники
Выбери предмет
S
А
Б
В
Г
И
К
М
П
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
С
Т
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства
Ф
Э