Условие:
Дана матрица переходных вероятностей марковской цепи с дискретным временем.
a) Составить граф марковской цепи.
б) Найти вероятности переходов из одного состояния в другое за два шага.
в) Определить финальные вероятности, если они существуют, а в противном случае доказать, что данная цепь не является регулярной.
г) Определить распределение вероятностей системы за один и два шага, если начальное распределение имеет вид Q(0)=(1;0;0) .
д) Найти стационарное распределение вероятностей.
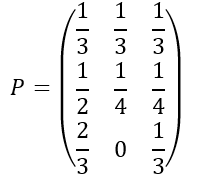
Решение:
Для описания цепи Маркова удобно использовать граф вероятностей переходов, вершины которого обозначают возможные состояния системы, стрелки от одной вершины к другой указывают возможные переходы между состояниями, а число над стрелкой задаёт вероятность такого перехода.
В задаче множество состояний X={1,2,3}, матрица вероятностей переходов имеет вид
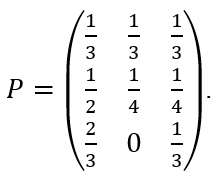
Тогда граф вероятностей переходов выглядит следующ...
