Дана система линейных уравнений, доказать ее совместность и решить тремя способами: 1) методом Гаусса 2) по формулам Крамера
«Дана система линейных уравнений, доказать ее совместность и решить тремя способами: 1) методом Гаусса 2) по формулам Крамера»
- Высшая математика
Условие:
Дана система линейных уравнений, доказать ее совместность и решить тремя способами:
1) методом Гаусса
2) по формулам Крамера
3) Средствами матричного исчисления
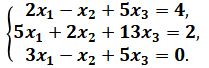
Решение:
Исследуем систему на совместность. Воспользуемся теоремой Кронекера-Капелли, для этого найдем ранг расширенной матрицы системы и ранг матрицы системы.
Найдем ранг матрицы методом элементарных преобразований. Ранг матрицы равен числу ненулевых строк в матрице после приведения её к ступенчатой форме при помощи элементарных преобразований над строками матрицы.
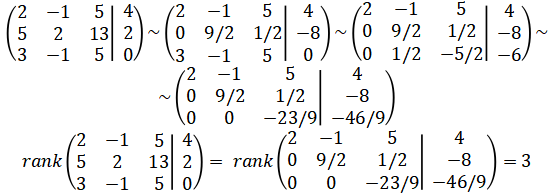
Ранг расширенной матрицы равен рангу матри...
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
AI помощники
Выбери предмет
S
А
Б
В
Г
И
К
М
П
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
С
Т
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства
Ф
Э