Дана выборка из генеральной совокупности объема. По выборке необходимо выполнить следующие расчеты. 1. Построить вариационный ряд. 2. Построить группированную выборку с числом интервалов .
- Высшая математика
Условие:
Дана выборка из генеральной совокупности объема. По выборке необходимо выполнить следующие расчеты.
1. Построить вариационный ряд.
2. Построить группированную выборку с числом интервалов k = 10.
3. Построить гистограмму и полигон частот.
4. По группированной выборке найти точечные оценки математического ожидания и среднеквадратического отклонения.
5. Построить доверительные интервалы для математического ожидания с доверительными вероятностями 0,95 и 0,99.
6. Выбрать один из законов распределения в качестве предполагаемого (теоретического) распределения, используя пункт 3.
7. Найти параметры теоретического распределения с помощью метода моментов. Построить на одном графике гистограмму, полигон частот и кривую теоретического распределения для найденных параметров.
8. Проверить гипотезу о том, что выборка имеет выбранное теоретическое распределение. Принять уровень значимости 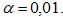

Решение:
1. Записав варианты в возрастающем порядке, получим вариационный ряд:
1,53 1,54 1,59 1,65 1,75 1,8 1,86 1,92 1,97 2,01 2,09 2,1 2,12 2,17 2,17 2,19 2,23 2,29 2,32 2,35 2,38 2,45 2,46 2,49 2,51 2,53 2,58 2,59 2,61 2,62 2,65 2,66 2,66 2,8 2,82 2,84 2,85 2,91 2,92 2,93 2,97 3,05 3,09 3,12 3,15 3,23 3,25 3,25 3,35 3,59
2. Объем выборки: 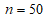 .
.
Находим среди выборки .
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
Выбери предмет
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Текстильная промышленность
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства