Решение задачи
Дана выборка объема 50 из неизвестного распределения. Постройте эмпирическую функцию распределения и гистограмму. Выдвинуть правдоподобную простую гипотезу о распределении. Проверить выдвинутую гипотезу с помощью критерия Колмогорова.
- Высшая математика
Условие:
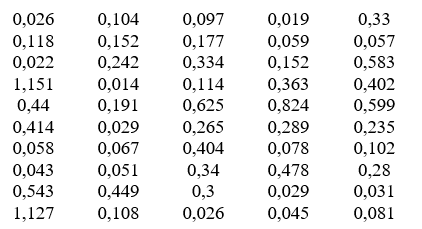
Дана выборка объема 50 из неизвестного распределения.
Таблица 1. Выборка неизвестного распределения
- Построить эмпирическую функцию распределения и гистограмму.
- Выдвинуть правдоподобную простую гипотезу о распределении.
Возможный набор:
а) E(θ), где θ =1,2,3,… целое;
б) R(0,θ), где θ =1,2,3,… целое;
в) N(θ,1), где θ =0,1,2,3,… целое. - Проверить выдвинутую гипотезу с помощью критерия Колмогорова и критерия Пирсона для уровня значимости α=0,05.
- Найти методом моментов и максимального правдоподобия теоретические оценки для неизвестных параметров распределения (в соответствии с выдвинутой гипотезой).
- Вычислить значения оценок для данной выборки.
Решение:
Упорядочим данную выборку в Excel и разобьем ее на интервалы, количество которых найдем по формуле Стерджеса:
![]()
Определим длину интервала:
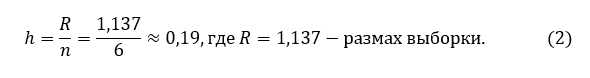
Составим интервальный ряд (таблица 2).
Таблица 2. Интервальный ряд
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
Выбери предмет
S
А
Б
В
Г
И
К
М
П
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
Р
С
Т
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Текстильная промышленность
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства
Ф
Э