Условие:
Дано уравнение 4x3 + x - 4/3 = 0
Требуется:
1) определить число корней уравнения и найти промежутки их изоляции;
2) вычислить значения одного из корней уравнения с точностью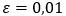 
при помощи метода деления отрезка пополам
Все промежуточные вычисления производить, используя не менее 4-х десятичных знаков после запятой.
Решение:
1) Будем искать такой интервал (a,b), в котором содержится корень уравнения 4x3 + x - 4/3 = 0 , причем только один.
Найдем производную 
. Так как для любых значений x, следует, что функция монотонно возрастающая, значит, уравнение имеет только один корень.