Условие:
Даны четыре вектора α = (3; 4; -3), b = (2; 1; -4), c = (-5; 5; 0), d = (8; -16; 17) в некотором базисе. Показать, что векторы α , b, c образуют базис, и найти координаты вектора d в этом базисе.
Решение:
Векторы будут линейно независимы, если определитель, составленный из этих векторов будет равен нулю.
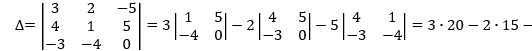
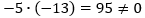
Следовательно, 3 вектора в пространстве линейно независимы и образуют базис.
