1. Главная
  2. Библиотека
  3. Высшая математика
  4. Даны координаты точек: A (1,-4,2), B(-3,0,6), C(-4,1,8), D(-1,0,2)                      Найдите: а) угол между ве...

Даны координаты точек: A (1,-4,2), B(-3,0,6), C(-4,1,8), D(-1,0,2)                      Найдите: а) угол между векторами и  ; б) площадь треугольника АВС; в) объем треугольной пирамиды с основанием АВС;

«Даны координаты точек: A (1,-4,2), B(-3,0,6), C(-4,1,8), D(-1,0,2)                      Найдите: а) угол между векторами и  ; б) площадь треугольника АВС; в) объем треугольной пирамиды с основанием АВС;»
  • Высшая математика

Условие:

Даны координаты точек:

A (1,-4,2), B(-3,0,6), C(-4,1,8), D(-1,0,2)                     

Найдите:

а) угол между векторам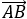и и  ;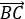

б) площадь треугольника АВС;

в) объем треугольной пирамиды с основанием АВС;

г) высоту, опущенную из вершины D на сторону AB;

д) уравнение прямой AB;

е) уравнение плоскости АВС.

Решение:

Предварительно найдем:

Координаты векторов.

Координаты векторов находим по формуле:

X = xj - xi; Y = yj - yi; Z = zj - zi

здесь X,Y,Z координаты вектора; xi, yi, zi - координаты точки Аi; xj, yj, zj - координаты точки Аj;

Например, для вектора AB

X = x2 - x1; Y = y2 - y1; Z = z2 - z1

X = -3-1; Y = 0-(-4); Z = 6-2

AB(-4;4;4)

AC(-5;5;6)

AD(-2;4;0)

BC(-1;1;2)

BD(2;0;-4)

CD(3;-1;-6)

Модули векторов (длина ребер пирамиды)

Длина вектора a(X;Y;Z) выражается через его координаты формулой:

Похожие задачи

Не нашел нужную задачу?

Воспользуйся поиском

AI помощники

Выбери предмет

E
S
А
Б
В
Г
Д
Е
Ж
З
И
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Э
Я