Условие задачи
Даны координаты вершин пирамиды. Найти:
1) длину ребра A1A2;
2) косинус угла между ребрами A1A2 и A1A4;
3) площадь грани A1A2A3;
4) уравнение грани A1A2A3;
5) уравнение высоты, опущенной из вершины A4 на грань A1A2A3;
6) объём пирамиды;
7) сделать чертёж.
A1 (3;-5;0), A2 (4;3;2), A3 (-1;1;4), A4 (4;5;-1)
Ответ
1) Длину ребра A1A2 найдём как длину вектора A1A2 ̅
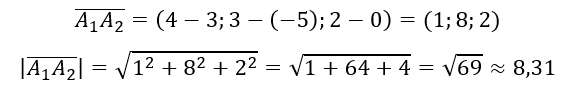
2) Косинус угла между ребрами A1A2 и A1A4 находим как косинус угла между соответствующими векторами, пользуясь определением скалярного произведения, получаем:









