Условие задачи
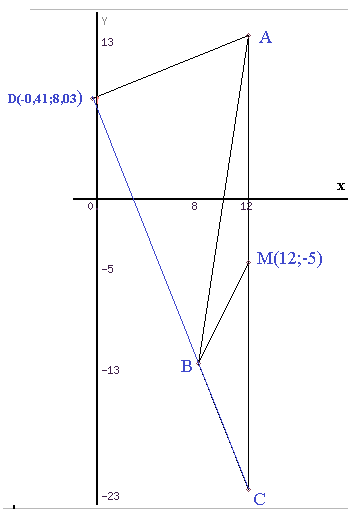
Даны координаты вершин треугольника А, В и С: A(12,13), B(8,-13), C(12,-23).
Требуется построить треугольник в декартовой системе координат и найти:
- уравнение и длину стороны АВ;
- тангенс угла А;
- уравнение и длину высоты АD;
- уравнение и длину медианы ВЕ;
- площадь треугольника АВС по координатам его вершин.
В ответах для всех нецелых числовых значений следует использовать десятичную дробь с округлением до 2-го знака после запятой.
Ответ
1) Координаты векторов.
Координаты векторов находим по формуле:
X = xj - xi; Y = yj - yi
здесь X,Y координаты вектора; xi, yi - координаты точки Аi; xj, yj - координаты точки Аj
Например, для вектора AB
X = x2 - x1; Y = y2 - y1
X = 8-12 = -4; Y = -13-13 = -26
AB(-4;-26)
AC(0;-36)
BC(4;-10)
Потяни
