Условие задачи
Даны вершины треугольника ABC: A(-6,1),B(-3,-5),C(0,-1).
Найти:
1. периметр и площадь треугольника (площадь вычислять по 2-м формулам: через определители 2-го и 3-го порядка);
2. уравнения сторон AB, AC и BC (общее, с угловым коэффициентом, параметрическое, в отрезках); координаты точек пересечения этих прямых с координатными осями;
3. уравнение прямой, проходящей через вершину C параллельно стороне AB;
4. уравнение высоты CH;
5. уравнение медианы AM;
6. координаты точки N пересечения высоты CH и медианы AM;
7. координаты точки D пересечения медиан (по 2-м формулам: деления отрезка в заданном отношении и как центра тяжести точек A,B,C);
8. длину высоты CH (2-мя способами: используя нормальное уравнение прямой AB и через площадь треугольника);
9. угол BAM по 2-м формулам: через тангенс и косинус угла между прямыми (сравнить); углы (в градусах) треугольника (3-мя способами: через косинус, тангенс и синус угла (сравнить));
10. уравнение окружности, описанной около треугольника, ее радиус и координаты центра.
Ответ
1) Найдем длины сторон треугольника по формулам:
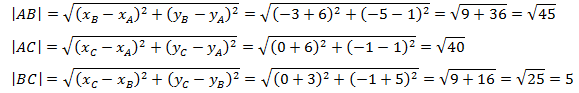
Тогда периметр треугольника:
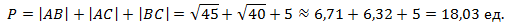
Найдем площадь треугольника по формулам:
1 способ:
