Решение задачи
Дифференциальная функция распределения СВ X имеет вид f(x) = A·g(x) при x1 ≤ x ≤ x2 и f(x) = 0 вне этого интервала. Требуется: а) найти коэффициент A;
- Высшая математика
Условие:
Дифференциальная функция распределения СВ X имеет вид f(x) = A·g(x) при x1 ≤ x ≤ x2 и f(x) = 0 вне этого интервала. Требуется:
а) найти коэффициент A;
б) найти M(X), D(X), σ(X);
в) найти функцию распределения F(x);
г) построить графики F(x) и f(x), рассматривая не менее 5 точек на интервале [x1; x2];
д) найти вероятность попадания СВ X в интервал (x1; (x1 + x2) / 2).
g(x) = x / (x2 + 1); [x1; x2] = [1; 3].
Решение:
Запишем дифференциальную функцию распределения в соответствии с условием задачи:

а). Одно из свойств плотности распределения вероятностей выражается следующей формулой:
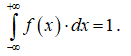
Исходя из этого свойства, можно о...
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
Выбери предмет
S
А
Б
В
Г
И
К
М
П
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
Р
С
Т
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Текстильная промышленность
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства
Ф
Э