Условие:
Для функции
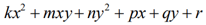
найти частные производные и дифференциалы 1-го и 2-го порядков,
производную по направлению вектора
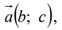
приближенное значение в точке
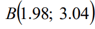
с помощью дифференциала,
экстремумы,
наибольшее и наименьшее значения в замкнутой области
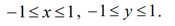
![]()
Решение:
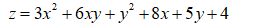

Для функции
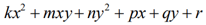
найти частные производные и дифференциалы 1-го и 2-го порядков,
производную по направлению вектора
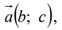
приближенное значение в точке
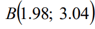
с помощью дифференциала,
экстремумы,
наибольшее и наименьшее значения в замкнутой области
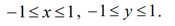
![]()
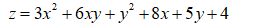
Не нашел нужную задачу?