Условие задачи
Для произвольных множеств A, B, C докажите утверждение либо приведите контр пример и проиллюстрируйте его диаграммой Эйлера-Венна.
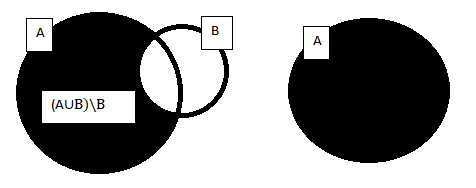
а) (A∪B)\B=A;
б) A\(B∩C)=(A\B)∪(A\C);
в) A∩(B∪C)=(A∩B)\C;
г) ¯(A∩B)=¯A∪¯B;
д) (A∪B)\(A∩B)=(A\B)∪(B\A);
е) (A∪B)\C=(A\C)∪(B\C);
ж) A∩(B\C)=(A∩B)\(A∩C);
з) A\(B\C)=(A\B)∪(A∩C).
Ответ
а) Если множества A и B имеют общие элементы, то эти элементы не принадлежат (AB)\B (как элементы множества B), но принадлежат множеству A (как элементы множества A). Значчит множества (AB)\B и A не равны ( в одном есть то, чего нет в другом).