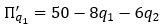1. Главная
  2. Библиотека
  3. Высшая математика
  4. Для товаров x1 и x2 известны функции спроса q1=q1 (p1 ) и q2=q2 (p2 ) где p1 и p2 цена единицы товара x1 и x2 соответствен...

Для товаров x1 и x2 известны функции спроса q1=q1 (p1 ) и q2=q2 (p2 ) где p1 и p2 цена единицы товара x1 и x2 соответственно. Фирма монополист имеет функцию издержек C=C(q1;q2) . Вычислить максимальную прибыль фирмы в этих условиях и найдите

«Для товаров x1 и x2 известны функции спроса q1=q1 (p1 ) и q2=q2 (p2 ) где p1 и p2 цена единицы товара x1 и x2 соответственно. Фирма монополист имеет функцию издержек C=C(q1;q2) . Вычислить максимальную прибыль фирмы в этих условиях и найдите»
  • Высшая математика

Условие:

Для товаров x1  и x2 известны функции спроса q1=q1 (p1 ) и  q2=q2 (p2 ) где p1 и p2 цена единицы товара x1  и x2 соответственно. Фирма монополист имеет функцию издержек C=C(q1;q2) . Вычислить максимальную прибыль фирмы в этих условиях и найдите соответствующий производственный план.

q1 = 25 - ½ p1

q2 = 39 / 2 - ½ p2

C = 2q12 + 6 q1 q2+ ½ q22+5

 

Решение:

Прибыль фирмы:

П(q1; q2 ) = p1 q1 + p2 q2 - C(q1; q2)

Цены из функций спроса:

q1 = 25 - p1 p1 = 50 - 2q1

q2 = 39 / 2 - p2 p2 = 39 - 2q2

Отсюда:

П(q1; q2) = (50 - 2q1) q1 + (39 - 2q2) q2-2q12-6q1 q2- q22 - 5 =

= 50q1 - 4q12 + 39q2 - 6q1 q2 - 2,5 q22 - 5

Похожие задачи

Не нашел нужную задачу?

Воспользуйся поиском

AI помощники

Выбери предмет

E
S
А
Б
В
Г
Д
Е
Ж
З
И
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Э
Я