Условие задачи
Длины сторон прямоугольника ― натуральные числа, а его периметр равен 200. Известно, что длина одной стороны прямоугольника равна n% от длины другой стороны, где n – также натуральное число.
а) Какое наибольшее значение может принимать площадь прямоугольника? Ответ обоснуйте.
б) Какое наименьшее значение может принимать площадь прямоугольника? Ответ обоснуйте.
в) Найдите все возможные значения, которые может принимать площадь прямоугольника, если дополнительно известно, что n>100. Ответ обоснуйте.
Ответ
а) Какое наибольшее значение может принимать площадь прямоугольника? Ответ обоснуйте.
а=x; b=0,01nx
S=ab=0,01nx2max
P=2(a+b)=2(x+0,01nx)=2x(1+0,01n)=200
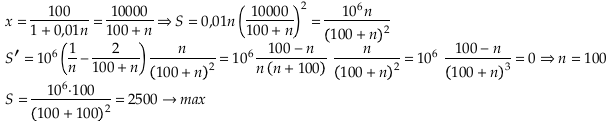
Наибольшее...
Потяни
