1. Главная
  2. Библиотека
  3. Высшая математика
  4. Доказать, что функционал в пространстве 𝐶[−1,1] является линейным непрерывным и найти его норму ‖𝐹‖.

Доказать, что функционал в пространстве 𝐶[−1,1] является линейным непрерывным и найти его норму ‖𝐹‖.

«Доказать, что функционал в пространстве 𝐶[−1,1] является линейным непрерывным и найти его норму ‖𝐹‖.»
  • Высшая математика

Условие:

Доказать, что функционал 

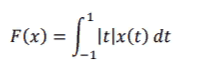
в пространстве 𝐶[−1,1] является линейным непрерывным и найти его норму ‖𝐹‖.

Решение:

Линейность функционала следует из линейности интеграла:

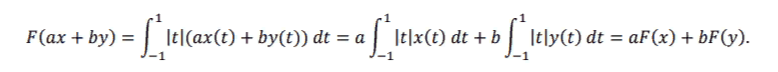
Функционал называется непрерывным тогда и только тогда, когда он переводит сходящиеся последовательности в сходящиеся:

из 𝑥𝑛 𝑥 следует 𝐹(𝑥𝑛) 𝐹(𝑥) для любой 𝑥𝑛.

На пространстве 𝐶[1,1] сходимость последовательности 𝑥𝑛 𝐶[1,1] означает

Похожие задачи

Не нашел нужную задачу?

Воспользуйся поиском

AI помощники

Выбери предмет

E
S
А
Б
В
Г
Д
Е
Ж
З
И
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Э
Я