Доказать, что каждая из систем векторов (а) = (а1, а2,а3) и (b) = (b1, b2, b3), образует базис в пространстве R^3. Найти матрицу перехода от базиса (a) к базису (b) и координаты вектора
- Высшая математика
Условие:
Доказать, что каждая из систем векторов (а) = (а1, а2,а3) и (b) = (b1, b2, b3), образует базис в пространстве R^3. Найти матрицу перехода от базиса (a) к базису (b) и координаты вектора х в базисе (а) и (b), если известны его координаты в стандартном базисе (е) = (е1, е2, е3), где
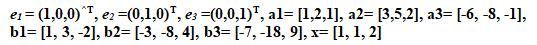
Решение:
Для того чтобы система векторов образовала базис в пространстве R^3, необходимо и достаточно, чтобы эти векторы были линейно независимы и любой вектор из R^3 мог быть выражен в виде их линейной комбинации.
Проверим, что система векторов (a) является базисом. Для этого найдем определитель матрицы, составленной из этих векторов:
| 1 2 1 |
| 3 5 2 |
|-6 -8 -1 |
Вычислим его по первой строке:
det = 1 * (5*(-1) - 2*(-8)) - 2 * (3*(-1) - 2*(-6)) + 1 * (-83 - 5(-6)) = -4
Так как определитель не равен нулю, система векторов (a) является базисом в пространстве R^3.
Аналогично проверим, что система векторов...
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
AI помощники
Выбери предмет
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства