Доказать, что система многочленов образует базис в пространстве Р2. Выписать в этом базисе столбец координат многочлена
«Доказать, что система многочленов образует базис в пространстве Р2. Выписать в этом базисе столбец координат многочлена»
- Высшая математика
Условие:
Доказать, что система многочленов
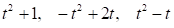
образует базис в пространстве Р2.
Выписать в этом базисе столбец координат многочлена
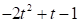
Решение:
Пространство Р2 ‒ множество многочленов степени не выше 2-х.
Любые три линейно независимых многочлена степени не выше 2-х образуют базис этого пространства.
Заданные многочлены
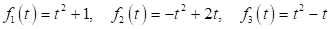
- многочлены второй степени.
Докажем их линейную независимость по определению.
Составим их линейную комбинацию, равную нулевому элементу пространства нулю:
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
AI помощники
Выбери предмет
S
А
Б
В
Г
И
К
М
П
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
С
Т
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства
Ф
Э