Условие задачи
Доказать, что векторы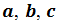 образуют базис. Разложить вектор
образуют базис. Разложить вектор 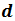 по этому базису:
по этому базису: 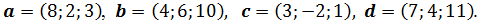
Ответ
Чтобы данные векторы образовали базис, необходимо и достаточно отличие от нуля определителя, составленного из координат этих векторов:
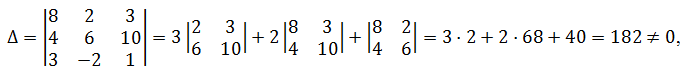
то есть данная система векторов образует некоторый базис. Разложение вектора по этому базису найде...









