Условие:
Доказать совместимость данной системы линейных уравнений и решить её тремя способами:
1) по формуле Крамера;
2) методом Гаусса;
3) средствами матричного исчисления.
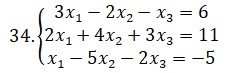
Решение:
По теореме Кронекера Капелли система совместна тогда и только тогда, когда ранг расширенной матрицы равен рангу основной матрицы системы.
Составим расширенную матрицу и методом элементарных преобразований найдём ранги матриц, получим:
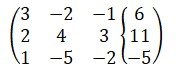
Умножим первую строку матрицы на (-2/3) и прибавим ко второй строке:
