Если на отрезке существования корня знаки f'(x) и f''(x) не изменяются, то в качестве начального приближения, обеспечивающего сходимость, выбираем тот конец отрезка, для которого знак функции f(x) совпадает со знаком ее второй производной f''(x).
«Если на отрезке существования корня знаки f'(x) и f''(x) не изменяются, то в качестве начального приближения, обеспечивающего сходимость, выбираем тот конец отрезка, для которого знак функции f(x) совпадает со знаком ее второй производной f''(x).»
- Высшая математика
Условие:
Дан многочлен третьей степени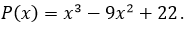 
Методом Ньютона найти действительный корень многочлена, расположенный на интервале (-3, 0) с точностью 
.
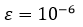Решение:
Проверим наличие корня на интервале (-3,0):
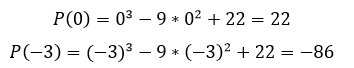
Если на отрезке существования корня знаки f'(x) и f''(x) не изменяются, то в качестве начального приближения, обеспечивающего сходимость, выбираем тот конец отрезка, для которого знак функции f(x) совпадает со знаком ее второй производной f''(x).
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
AI помощники
Выбери предмет
S
А
Б
В
Г
И
К
М
П
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
С
Т
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства
Ф
Э