1. Главная
  2. Библиотека
  3. Высшая математика
  4. Фабрика по производству мороженого может выпускать два сорта мороженого: молочное и сливочное. При производстве мороженого...

Фабрика по производству мороженого может выпускать два сорта мороженого: молочное и сливочное. При производстве мороженого используют три вида сырья

«Фабрика по производству мороженого может выпускать два сорта мороженого: молочное и сливочное. При производстве мороженого используют три вида сырья»
  • Высшая математика

Условие:

Фабрика по производству мороженого может выпускать два сорта мороженого: молочное и сливочное. При производстве мороженого используют три вида сырья: молоко, дешевые наполнители и дорогие наполнители, запасы которых составляют 5 т, 3 т и 5,7 т соответственно. Известны удельные затраты сырья для каждого из сортов и цены продукции. Для молочного мороженого они составляют 0,5 кг,0,1 кг и 0,4 на 1 кг мороженого, а для сливочного – 0,2 кг, 0,3 и 0,5 кг на 1 кг мороженого. Цена молочного мороженого составляет 200 рублей за 1 кг, а сливочного – 300 рублей за 1 кг.

Требуется построить план производства, который обеспечивает максимум дохода, и найти оптимальный доход.

Решение:

Пусть х1,х2 количество молочного и сливочного соответственно, кг. Тогда математическая модель задачи запишется таким образом
Найти значения переменных x1...x2, при которых функция:

Q = 200 x1 + 300 x2

принимает максимальное значение, при условии следующих ограничений:

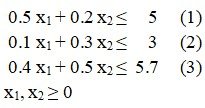
Шаг:1

Избавимся от неравенств в ограничениях, введя в ограничения 1, 2, 3 неотрицательные балансовые переменные s1, s2, s3.

Похожие задачи

Не нашел нужную задачу?

Воспользуйся поиском

AI помощники

Выбери предмет

E
S
А
Б
В
Г
Д
Е
Ж
З
И
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Э
Я