Условие задачи
Фирма имеет возможность рекламировать свою продукции, используя местные радио- и телевизионную сеть. Затраты на рекламу в бюджете фирмы ограничены $1000 в месяц. Каждая минута радиорекламы обходится в $5, а минута телерекламы – в $100. Фирма хотела бы использовать радиосеть, по крайней мере, в два раза чаще, чем сеть телевидения. Опыт прошлых лет показал, что объем сбыта, который обеспечивает каждая минута телерекламы, в 25 раз больше сбыта, обеспечиваемого одной минутой радиорекламы.
Определить оптимальное распределение ежемесячно отпускаемых средств между радио- и телерекламой.
Согласно исходным данным необходимо:
1. Составить математическую модель задачи линейного программирования.
2. Решить задачу линейного программирования в Excel с помощью программы "Поиск решения".
3. Определить оптимальный план выпуска продукции, максимальное значение целевой функции (прибыли) и соответствующее распределение ресурсов.
Ответ
1. Составим математическую модель задачи линейного программирования.
Обозначим через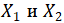 
количество ежемесячно отпускаемых средств на радио- и телерекламу соответственно. Тогда количество минут, используемых для радиорекламы, будет равно , а количество минут, используемых для телерекламы, будет равно . Согласно условию задачи получим следующие ограничения на количество денежных средств.
