Условие:
Геометрическое приложение тройного интеграла. Найти массу тела, ограниченного поверхностями
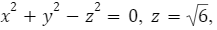если плотность в каждой точке равна аппликате этой точки.
Решение:
Масса участка поверхности S находится как поверхностный интеграл первого рода
Поверхность S часть конуса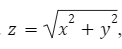 
заключенная между плоскостями .