Условие задачи
Имеется m складских помещений (пунктов отправления) A1,A2,…,Am, в которых сосредоточены запасы груза в количествах a1,a2 ,…, am единиц соответственно, и n пунктов назначения B1,B2 ,…,Bn , подавших заявки соответственно на b1,b2,…, bn единиц указанного груза. Известна тарифная матрица C , в которой ci,j – стоимость перевозки одной единицы груза из склада Ai в пункт назначения B j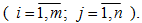 
Найти план перевозок учитывающий запасы груза на складах и объемы заявок пунктов назначения, имеющий наименьшую общую стоимость. Исходные данные задачи занесены в следующую таблицу
a. Построить математическую модель организации перевозок: записать оптимизационную задачу, дать экономическую интерпретацию вводимых переменных.
b. Записать двойственную задачу, к построенной задаче линейного программирования.
c. Составить начальный план перевозок по методам северо-западного угла и наименьшей стоимости. Укажите стоимости перевозок по этим планам.
d. Найти оптимальный план задачи по методу потенциалов и доказать его оптимальность по теореме двойственности.
Ответ
Проверим необходимое и достаточное условие разрешимости задачи:
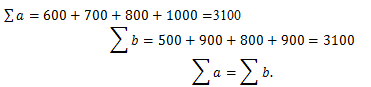
Суммарная потребность груза равна запасам груза у поставщиков. Следовательно, задача является закрытой.
Найдем начальное решение методом минимального элемента.
Минимальный элемент матрицы тарифов находится в ячейке A3B3 и равен 2. Запасы поставщика A2 составляют 700 ед. Потребность потребителя B3 составляет 800 ед. От поставщика A2 к пот...
