Условие задачи
Исследовать данные функции методами дифференциального исчисления и построить их графики. Исследование функции рекомендуется проверить по следующей схеме:
1) найти область определения функции;
2) исследовать функцию на непрерывность;
3) определить. является ли данная функция четной, нечетной;
4) найти интервалы возрастания и убывания функции н точки ее экстремума;
5) найтиинтервалы выпуклости и вогнутости графика функции и точки перегиба;
6) найти асимптоты графика функции.
Ответ
1. Область определения функции: x принадлежит любому значению , так как x2+3 не равно 0 при всех действительных числах.
2. Функция непрерывна
3. Четность или нечетность функции.
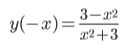
y(-x) = y(x), четная функция
4. Исследование на экстремум.
Находим интервалы возрастания и убывания. Первая производная.
