Исследовать ряды на сходимость. В задании 4 оценить сумму ряда после третьего члена. ∑_(n=1)^∞(2n-1)/(3n+1) ∑_(n=1)^∞(2n+5)/(n^3+8)∑_(n=1)^∞2^n/(n∙3^(n-1) ) ∑_(n=1)^∞((-1)^n∙n^3)/(n^4+1)
«Исследовать ряды на сходимость. В задании 4 оценить сумму ряда после третьего члена. ∑_(n=1)^∞(2n-1)/(3n+1) ∑_(n=1)^∞(2n+5)/(n^3+8)∑_(n=1)^∞2^n/(n∙3^(n-1) ) ∑_(n=1)^∞((-1)^n∙n^3)/(n^4+1)»
- Высшая математика
Условие:
Исследовать ряды на сходимость. В задании 4 оценить сумму ряда после третьего члена.
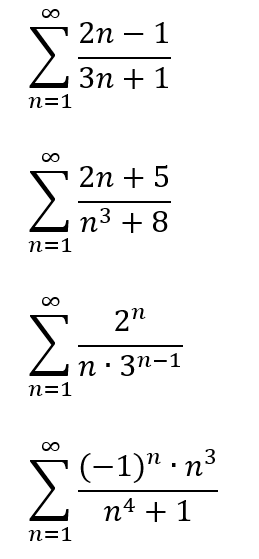
Решение:
1) Проверим выполнимость необходимого признака сходимости:
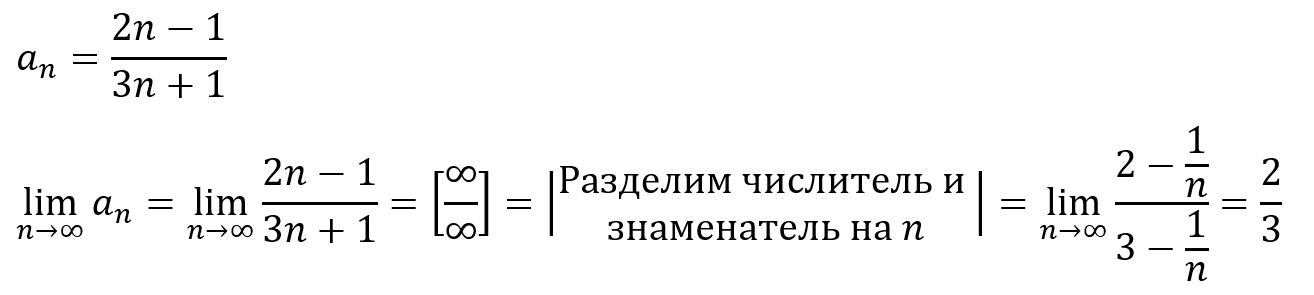
Так как общий член ряда не стремится к нулю, то необходимый признак сходимости ряда не выполняется и ряд расходится.
2) Сравним данный ряд со сходящимся, обобщенно гармоническим рядом, с показателем степени =2
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
AI помощники
Выбери предмет
S
А
Б
В
Г
И
К
М
П
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
С
Т
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства
Ф
Э