Из генеральной совокупности извлечена выборка. Данные наблюдений сведены в группы и представлены в виде дискретного вариационного ряда, где первая строка – середины Требуется выполнить статистическую обработку экспериментальных данных по следующей схеме
- Высшая математика
Условие:
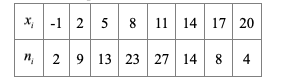
Из генеральной совокупности извлечена выборка. Данные наблюдений сведены в группы и представлены в виде дискретного вариационного ряда, где первая строка – середины
 Требуется выполнить статистическую обработку экспериментальных данных по следующей схеме
Требуется выполнить статистическую обработку экспериментальных данных по следующей схеме
1) Построить выборочную (эмпирическую) функцию распределения F*(x)
2) Построить полигон и гистограмму относительных частот
3) Найти числовые характеристики выборки: выборочную среднюю , выборочное среднее квадратическое отклонение σ, исправленное среднее квадратическое отклонение S
4) Сделать предварительный выбор закона распределения по виду гистограммы и полигона относительных частот
5) Проверить с помощью критерия согласия Пирсона гипотезу о нормальном законе распределения генеральной совокупности при уровне значимости α = 0,05
6) В случае принятия гипотезы о нормальном законе распределения найти интервальные оценки параметров нормального распределения (доверительную вероятность принять равной γ =1−α = 0,95 ). Вычисления проводить с точностью до 0,001.
Решение:
1)Объем выборки равен 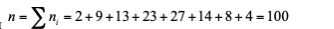
Запишем эмпирическую функцию распределения

Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
AI помощники
Выбери предмет
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства