Условие:
Из генеральной совокупности извлечена выборка. Данные наблюдений сведены в группы и представлены в виде дискретного вариационного ряда, где первая строка – середины частичных интервалов xi, вторая строка – соответствующие им частоты ni.

Требуется выполнить статистическую обработку экспериментальных данных по следующей схеме:
1) Построить выборочную (эмпирическую) функцию распределения F*(x);
2) Построить полигон и гистограмму относительных частот;
3) Найти числовые характеристики выборки: выборочную среднюю xв , выборочное среднее квадратическое отклонение σ, исправленное среднее квадратическое отклонение S;
4) Сделать предварительный выбор закона распределения по виду гистограммы и полигона относительных частот;
5) Проверить с помощью критерия согласия Пирсона гипотезу о нормальном законе распределения генеральной совокупности при уровне значимости;
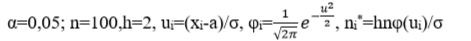
6) В случае принятия гипотезы о нормальном законе распределения найти интервальные оценки параметров нормального распределения (доверительную вероятность принять равной γ=0,95).
Решение:
| 1) |
