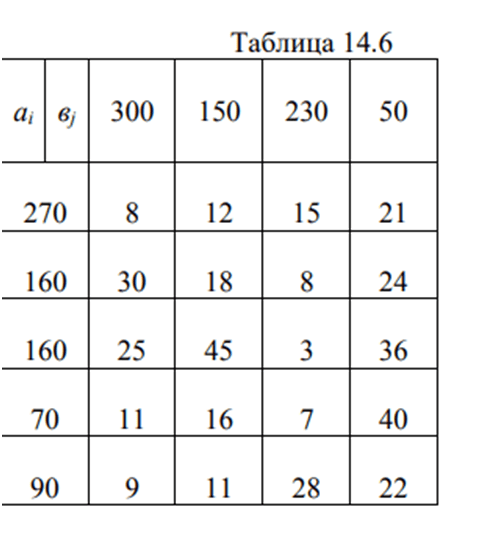
Из m пунктов хранения требуется доставить однородный груз в n пунктов потребления. Количество единиц груза в каждом пункте отправления, объемы потребления даны в таблице.
- Высшая математика
Условие:
Из m пунктов хранения( или производства) требуется доставить однородный груз в n пунктов потребления. Количество единиц груза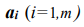 
в каждом пункте отправления, объемы потребления 
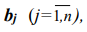а также стоимости перевозки единицы груза из i-го пункта производства в j-й пункт потребления даны в таблице.
Составить математическую модель транспортной задачи.
Найти оптимальный план перевозки двумя способами.
Решение:
Проверим необходимое и достаточное условие разрешимости задачи.
a = 270 + 160 + 160 + 70 + 90 = 750
b = 300 + 150 + 230 + 50 = 730
Как видно, суммарная потребность груза в пунктах назначения меньше запасов груза на базах. Следовательно, модель исходной транспортной задачи является открытой. Чтобы получить закрытую модель, введем дополнительную (фиктивную) потребность, равной 20 (750730). Тарифы перевозки единицы груза к этому магазину полагаем равны нулю.
Занесем исходные данные в распределительную таблицу.
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
AI помощники
Выбери предмет
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства