Измерялось усилие резания при черновой обточке литой заготовки из серого чугуна. При этом были получены следующие результаты (в кто):Длина интервала h=4. Провести статистическую обработку результатов испытании.Схема решения:

25 июля 2024
Высшая математика

Условие:

Измерялось усилие резания при черновой обточке литой заготовки из серого чугуна. При этом были получены следующие результаты (в кто):

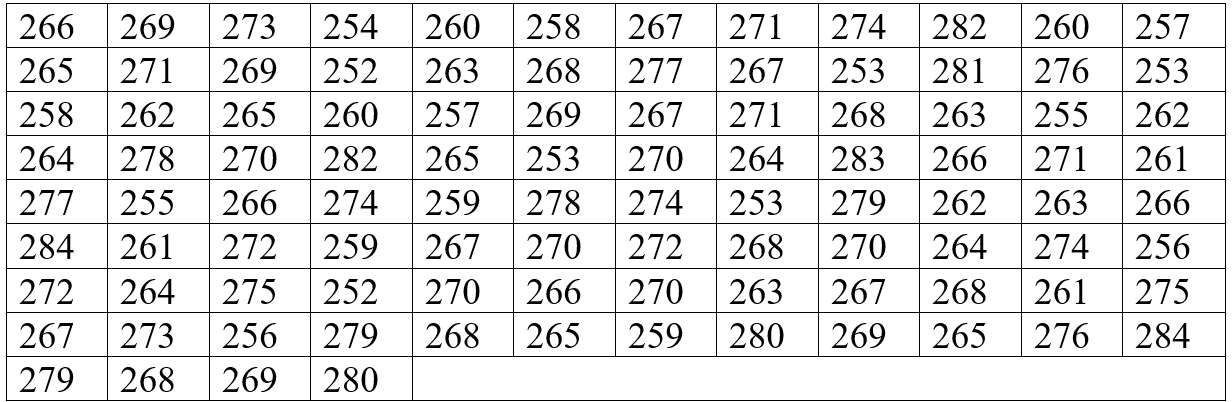
Длина интервала h=4.

Провести статистическую обработку результатов испытании.

Схема решения:

1. Составить интервальный ряд распределения.

2. Построить гистограмму.

3. Вычислить оценки математического ожидания (М.О) и средне квадратичного ожидания (С.К.О.)

4. Построить доверительный интервал для М.О. и С.К.О. с надежностью (доверительной вероятностью)

γ=0,95.

5. Используя критерий согласия (Пирсона) выяснить не противоречит ли принятая гипотеза о виде закона распределения опытным данным.

6. Построить кривую нормального закона, совместив её с графиком гистограммы распределения, приведя в соответствие масштабы.

Решение:

По данным выборки строим интервальный вариационный ряд. Находим размах варьирования признака Х по формуле R = x_ma... - x. Просматривая исходные данные, находим x = 284, x= 252 . Тогда R = 284 - 252= 32. Подсчитываем число вариантов, попадающих в каждый интервал, по данным выборки. Значение xi, попадающее на границу интервала, относим к левому концу. За начало x0 первого интервала берем величину x = x - 0,5h = 252- 0,54= 250. Конец x последнего интервала находим по формуле x = x+ 0,5h = 284 + 0,5*4= 286. Сформированный интервальный вариационный ряд записываем в виде табл. 1.