Условие задачи
Известны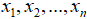 
- результаты независимых наблюдений над случайной величиной Х.
1. Сгруппировать эти данные в интервальную таблицу, подобрав длину интервала.
2. Построить гистограмму, полигон частот и эмпирическую функцию распределения.
3. Найти несмещённые оценки для математического ожидания и дисперсии случайной величины Х. Указать моду М0.
4. По критерию χ2 (Пирсона) проверить гипотезу о том, что случайная величина Х имеет нормальный закон распределения.
5. Найти интервальные оценки математического ожидания и дисперсии случайной величины Х с уровнем доверия γ=0,9.
85; 76; 80; 84; 88; 89; 91; 88; 84; 85; 75; 82; 86; 89; 88; 84; 90; 89; 85; 91; 87; 81; 78; 85; 88; 91; 89; 87; 74; 81; 87; 90; 88; 86; 76; 84; 88; 77; 82; 85; 84; 74; 80; 84; 91; 93; 90; 88; 87; 77; 83; 89; 89; 91; 92; 88; 94; 90; 88; 81; 83; 89; 94; 96; 88; 95; 99; 90; 86; 78; 81; 86; 90; 92; 93; 90; 83; 79; 86; 90; 79; 82; 87; 85; 91; 97; 88; 85; 87; 90; 89; 95; 89; 84; 91; 89; 90; 98; 91; 88.
Ответ
1. Объем выборки n = 100.
Размах варьирования: R=xmax xmin= 99 - 74 = 25. Длину интервала (шаг) определим следующим образом:
H=R/5=25/5=5.
Начало первого интервала xmin = 74.
Объединим в таблицу интервальный и дискретный вариационные ряды:
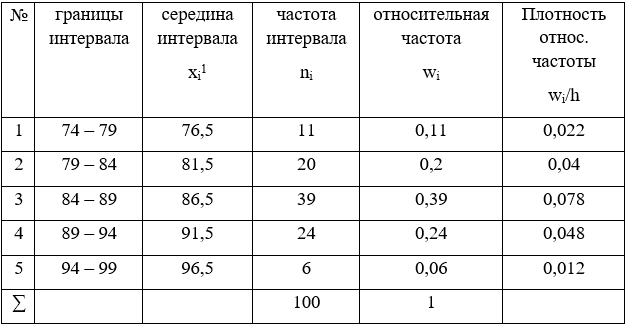
2.
