Условие задачи
Множество Кантора строится следующим образом: 𝐶0 = [0, 1], а
для построения 𝐶𝑛+1 нужно каждый из отрезков, входящих в 𝐶𝑛, разбить на три
равные части и выбросить интервал, составлющий среднюю треть. Например,
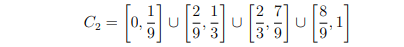
Тогда множество Кантора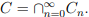 
Ковер Серпинского строится аналогично множеству Кантора, только начинаем с единичного квадрата 𝑆0 = [0, 1] × [0, 1]. На очередном шаге делим каждый входящий квадрат на 9 равных квадратов и выбрасываем средний квадрат без границы.
(a) Постройте 𝑆1, 𝑆2. Сформулируйте определение аналогично множеству Кан-
тора и введите объект аналогичный 𝐺𝑛.
(b) Найдите площадь ковра Серпинского.
(c) Как по троичной записи координат (𝑥, 𝑦), 𝑥, 𝑦 ∈ [0, 1] понять, принадлежит ли точка ковру Серпинского или нет?
Ответ
(a) Согласно описанию,
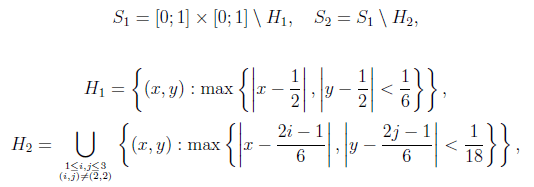
b) Заметим, что 
. Как нетрудно видеть,
