Условие задачи
Задано 10 населённых пунктов, связанных сетью. Расстояние между пунктами указано в километрах.
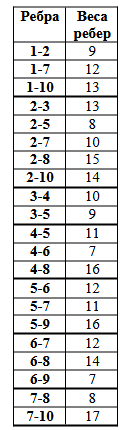
Задача № 1. Определить номера населённых пунктов, размещение телефонных станций в которых будет оптимальным по удалённости от самого дальнего пункта.
Задача № 2. Найти минисуммное решение задачи размещения 5-и телефонных станций из предложенных вариантов:
Задача № 3. Определить, по каким кабельным линиям работник станции P (таблица 1) пройдёт дважды в поисках повреждений на линии. Предложить вариант оптимального маршрута.
Задача № 4. Определить, как проложить телефонный кабель от пункта p1 до пунктов p2 и p3 и между пунктами p2 и p3 (таблица 1), чтобы затраты на прокладку кабеля были минимальными. Рассчитать минимальные суммарные затраты, если стоимость 1 км кабеля – 11 единиц. p1 = 1, p2 = 4, p3 = 9
Задача № 5. Построить сеть с минимальной суммарной стоимостью кабельных соединений. Определить затраты на кабель, если стоимость 1 км кабеля составляет 10 единиц.
Задача № 6. Заданный граф представляет модель вторичной сети связи, веса рёбер которого являются пропускными способностями соответствующих каналов. Определить пропускную способность сети между узлами 3 и 10
Ответ
Задача № 1.
1. Составим матрицу расстояний, элементами которой являются расстояния между вершинами (длина кратчайшего пути).
2. Определим эксцентриситеты вершин (максимальное из расстояний от определённой вершины):
