Методом Лагранжа аппроксимировать функцию, заданную таблично. Построить график полученной функции Лагранжа, на графике отметить заданные точки аппроксимации.
«Методом Лагранжа аппроксимировать функцию, заданную таблично. Построить график полученной функции Лагранжа, на графике отметить заданные точки аппроксимации.»
- Высшая математика
Условие:
Методом Лагранжа аппроксимировать функцию, заданную таблично. Количество точек аппроксимации равно шесть. Абсциссы точек для всех вариантов принять равными: 0; 0,5; 1; 2; 3,5; 4; 6. Массив ординат представлен в таблице 4.1. Построить график полученной функции Лагранжа, на графике отметить заданные точки аппроксимации.
Таблица 4.1.
Данные к заданию 1
| Вариант | 1 точка | 2 точка | 3 точка | 4 точка | 5 точка | 6 точка | 7 точка |
| 18 | –15,828 | 1,396 | 34,206 | 82,917 | 57,901 | 98,128 | 123,178 |
Решение:
Интерполяционный многочлен Лагранжа L(x) на сетке {xi}, i=0..n имеет вид:
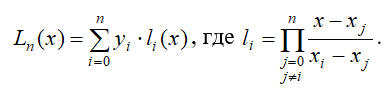
По условиям задания х0=0, х1=0.5, х2=1, х3=2, х4=3.5, х5=4, х6=6.
Находим базисные многочлены li (x):
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
AI помощники
Выбери предмет
S
А
Б
В
Г
И
К
М
П
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
С
Т
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства
Ф
Э