1. На базисе е1,е2, е3 заданы векторы а1 равно (1;1;0), а2 равно (1; -1;1) и а3 равно ( -3;5; -6). Показать, что векторы а1, а2, а3 образуют базис. 2. Даны векторы а равно (2; -1;-2) и б равно (8; -4;0). Найти скалярное произведение векторов.
«1. На базисе е1,е2, е3 заданы векторы а1 равно (1;1;0), а2 равно (1; -1;1) и а3 равно ( -3;5; -6). Показать, что векторы а1, а2, а3 образуют базис. 2. Даны векторы а равно (2; -1;-2) и б равно (8; -4;0). Найти скалярное произведение векторов.»
- Высшая математика
Условие:
1. На базисе е1, е2, е3 заданы векторы а1=(1;1;0), а2=(1;-1;1) и а3=(-3;5;-6). Показать, что векторы а1, а2, а3 образуют базис.
2. Даны векторы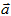 
=(2;-1;-2) и 
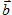=(8;-4;0). Найти скалярное произведение векторов 
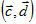, где 
Решение:
1. Три вектора образуют базис в пространстве, если они некомпланарные. Условием некомпланарности трех векторов является неравенство нулю их смешанного произведения. Проверим это условие для векторов заданных....
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
AI помощники
Выбери предмет
S
А
Б
В
Г
И
К
М
П
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
С
Т
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства
Ф
Э