Условие задачи
На координатной плоскости задан треугольник ABC координатами своих вершин. Требуется найти:
- уравнение стороны AB;
- уравнение высоты CD и вычислить ее длину;
- уравнение медианы BM, угол q между высотой CD и медианой BM.
A (8;5); B (3;7); C (6;5)
Ответ
1)Найдём уравнение стороны AB как уравнение прямой, проходящей через две точки, получим следующее каноническое уравнение:
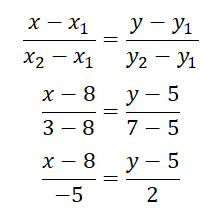
Также представим уравнение прямой AB с угловым коэффициентом, получим:
-5 * (y -5) = 2 * (x - 8)
-5y + 25 = 2x - 16
-5y = 2x - 41









