На отрезке [0; 2] методом Ньютона найти корень уравнения 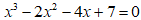x^3 - 2x^2 - 4x + 7 = 0 с точностью 0,0001 (ЭТ). Представим заданное уравнение в виде x^3 - 2x^2 = 4x - 7 и построим графики функций  g(x) = x3 - 2x2   и  h(x) = 4x - 7 .

Представим заданное уравнение в виде x³ - 2x² = 4x - 7 и построим графики функций g(x) = x³ - 2x² и h(x) = 4x - 7 . Отметим на чертеже корень x*:

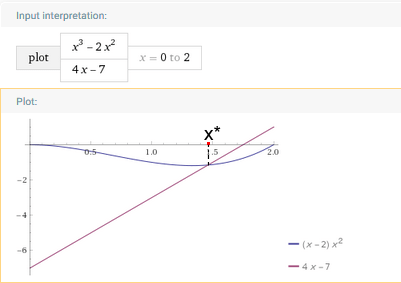
Теперь выберем начальное приближение корня x₀, удовлетворяющее условию