Условие задачи
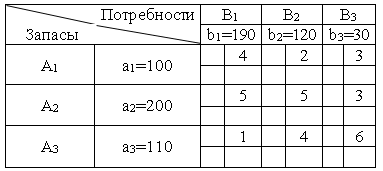
На трех складах A1, A2 и A3 хранится a1 = 100, a2 = 200 и a3 = 110 единиц одного и того же груза. Этот груз требуется доставить трем потребителям B1, B2 и B3, заказы которых составляют b1 = 190, b2 = 120 и b3 = 30 единиц груза соответственно.
Стоимости перевозок cij единицы груза с i-го склада j-му потребителю указаны в правых верхних углах соответствующих клеток транспортной таблицы:
2.1. Сравнивая суммарный запас 
и суммарную потребность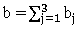 
в грузе, установить, является ли модель транспортной задачи, заданная этой таблицей, открытой или закрытой. Если модель является открытой, то её необходимо закрыть, добавив фиктивный склад A′4 с запасом a′4 = b – a в случае a < b или фиктивного потребителя B′4 с потребностью b′4 = a – b в случае a > b и положив соответствующие им тарифы перевозок нулевыми.
2.2. Составить первоначальный план перевозок. (Рекомендуется воспользоваться методом наименьшей стоимости).
2.3. Проверить, является ли первоначальный план оптимальным в смысле суммарной стоимости перевозок, и если это не так, то составить оптимальный план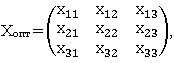 
обеспечивающий минимальную стоимость перевозок 
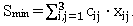Найти эту стоимость.
Ответ
2.1). Обеспечиваем условие разрешимости транспортной задачи.
В общем случае условие разрешимости транспортной задачи состоит в том, что сумма запасов поставщиков в m пунктах отправления (ПО) должна быть равна суммарной потребности потребителей в n пунктах назначения (ПН)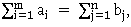 
то есть модель транспортной задачи должна быть закрытой.
Согласно условию задачи, имеем:
